Ways to Multiply

Some semesters I teach math methodology classes to preservice teachers (that means they are teachers in training). One of the mainstays of my courses is to push for more student involvement and ownership of the math content, that includes K-12 student involvement in the preservice teachers' future classes as well as undergraduate involvement in my classes. This really is supposed to look like students exploring and using what they know to figure out new problems, or sometimes using tools to find out for themselves how to do something new to them. That is a contrast to the "traditional" mode of teaching, where teachers tell students steps to solve problems, which I think only works for some students.

What I sometimes find is a hybrid between the traditional mode of teaching and a student-centered mode that can be analogous to a biological hybrid that is sterile and cannot reproduce (I'm looking at you, liger). It's not necessarily a bad thing that my undergraduates do this in the lessons they teach, because I see it as the next step in learning. Learning is more complex than the dichotomy of not knowing, and knowing. Learning sometime requires butting up against prior experiences and knowledge.

It is like students are standing between two teaching modalities, lecture-based, and exploratory. Most of their background knowledge lives in the lecture-based world, so providing K-12 students learning opportunities without telling them explicitly how to do it goes against every fiber of their experience. In some ways, I imagine it is like an adult trying to do a flip off a diving board for the first time without any training. Sometimes, there is a half-commitment to the flip, and the other half is the body trying to protect itself. The result is a spectacular belly- or back-flop

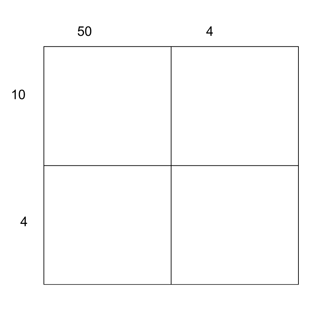
The brief example I want to share today is from a lesson plan a preservice teacher sent me. They wanted to have students solve 2-digit multiplication problems with area models. The plan's intention was to drive student discussion and invention of a solution without explicitly teaching that method. Let's say the problem was 54 x 14, their plan was to start by projecting on the board:

So there are good things happening here. The two numbers are decomposed to illustrate that 14 can be written as 10 and 4, and 54 can be decomposed as 50 and 4, this is an important feature of multiplying two-digit numbers. Then they wanted to ask students to work in small groups to figure out how to solve it in this way. Having never seen this method before, it seemed to me that the K-12 students would be confused if they were merely asked to take this image and find the product. What we see is an attempt to give students an opportunity to try and solve it without lecture, but the supports needed for students to do that are absent.

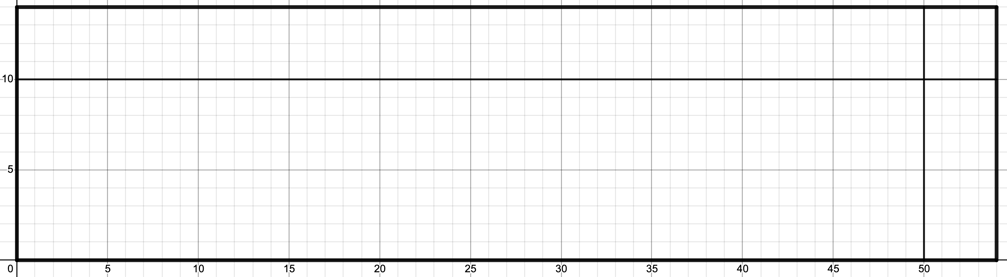
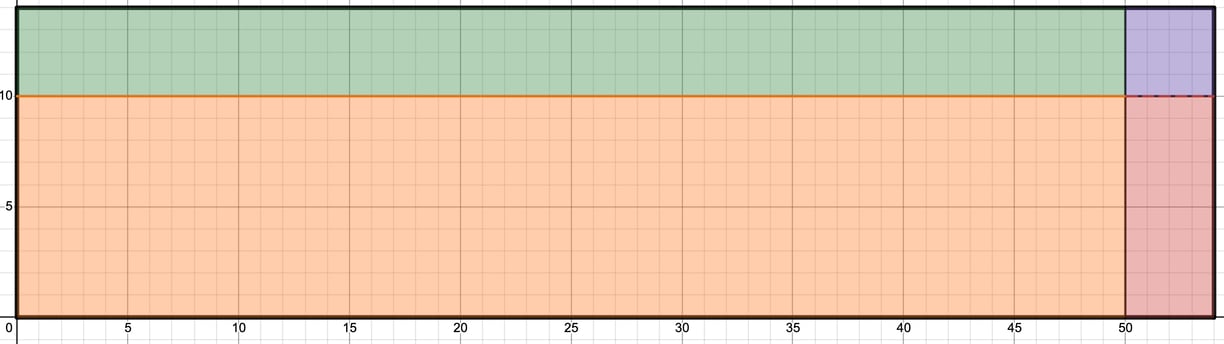
So I suggested the following image to consider instead:

This second image is different from the original in some important ways. First, students COULD figure out the area without using a method previously presented; maybe by counting squares, or finding patterns and using those patterns to count. Second, students might use the structure created here of the rectangle split into quadrants and find the area of each quadrant and add it all up and then come to the conclusion later that what they have done is (10+4)x(50+4) and could "create" the first proposed area model themselves. Third, and maybe most importantly, is that the size of each quadrant is appropriate for the decomposed number parts, a support not afforded in the original square with equal quadrants. This final point can illustrate to students a rationale for this method working. Even through lecture-based instruction, meaning can be made by the the size of the quadrants, rather than this method just becoming a rule to remember.

I hope this story illustrates the complexity of learning and the importance of making room for the learner to navigate the vast divide between two conceptions that are related by topic or name, but different in execution or behavior. It is not appropriate to expect a smooth transition from one conception to another.