Alice In-Equality Land

Long ago, I started writing a story about Alice (from Alice in Wonderland) in a world that was more obviously mathematical than Lewis Caroll's original story. I was teaching Algebra 2 and I found the topics to be procedure heavy and I was trying to find a way to develop a way to engage students with the math conceptually. At the time, the idea of this story began to brew and I went with it. I include a short excerpt from the story I have created and I will also include a Desmos classroom slide to demonstrate the actions regarding the concept. This excerpt occurs just after Alice falls into this strange new world (please note that Alice in Wonderland is part of the public domain, so I am not committing copyright infractions) and meets a few of the creatures that inhabit this land. A character: "Equal To" is the famous rabbit character.

Alice in-equality Land

After her soft landing, Alice looked around and saw she was standing in a new wooded area. As Alice walked through the forest she came upon two funny looking creatures with pointy noses and odd flat, flapping mouths. They were speaking to each other in loud hushed voices and gesticulated wildly. Upon seeing Alice approach, the two stopped arguing.

“Who are you?” asked one.

“Where thou come’st from shrew?” asked the other.

Alice was taken aback. “My name is Alice, I’m from… well, I don’t really know how to explain it.”

“You don’t know where you reside?” said one.

“Then how will you know where to hide?” asked the other.

“I don’t want to hide… Who are you?”

“Her comment might be construed as snide,” said the first.

“She dodges the question, methinks she lied.”

Alice took a step backwards, “I just wanted to know your names. I feel most at ease when I know someone’s name.”

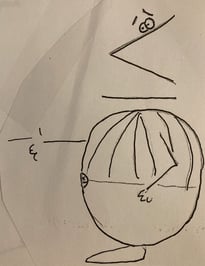
The two characters brightened up immediately. “In that case, I’m At Most, and he’s At Least.”

“No, I’m At Most, YOU’RE At Least! You beast.” Indeed, Alice noticed that their heads very closely resembled inequality signs.

“Oh, right,” At Least said. He turned to Alice, “your name sounds like mine, you should join us in the fight.”

Quick to catch the mistake, Alice replied, “My name is Alice, not Aleese!”

“At least enunciate when you speak your name,” said At Most.

“I did just the same!” replied At Least, angrily.

“I was speaking to the lass,” said At Most.

“Her name is Alace,” replied At Least.

Alice ignored his butchering of her name. “Your side?” Replied Alice. “What side might that be?”

“Well of course, the right side… or the left, maybe, it does not matter, whichever the case may be,” said At Most.

“I don’t understand, whom are you taking sides against?”

“Less Than and Greater Than,” said At Least.

“They are our rival clan,” said At Most.

“But why?” Implored Alice.

Almost as if Alice’s question was an entrance cue for a play, a giant caterpillar with a megaphone in one hand slowly inched out from behind a rock and cleared his throat. He began to read from a parchment, much like he was making a decree. As the caterpillar spoke each line, that action took place.

At Least and At Most challenged

Less Than and More Than to a duel,

For Less Than said that At Least

“Flipped his sign, that fool.”

They sized each other up and down

Checking again the position of their foe

Allies felt the shape of each other’s crown

Fists rose up, steady now, prepare for the first blow

But just before their rumble,

Equal To hopped in and intervened

He put the four signs in a jumble

And said, “this should please my Queen.”

Alice could not believe it, the rabbit she had followed through the brush was standing in front of her wearing a smock with two parallel lines on it… and he could talk! Right after solving the quarrel, the white rabbit jumped up and said, “no time to dawdle, I’ll be late!” and he ran off into the woods

Alice was intrigued, “late for what I wonder.”

At Most accepted the challenge to explain, “Equal To is always running around because he has to show up to things exactly on time, as the Queen demands, he cannot be early or late. I for example can show up early... er... late... well, it depends on how you look at it, but I can also always be on time.”

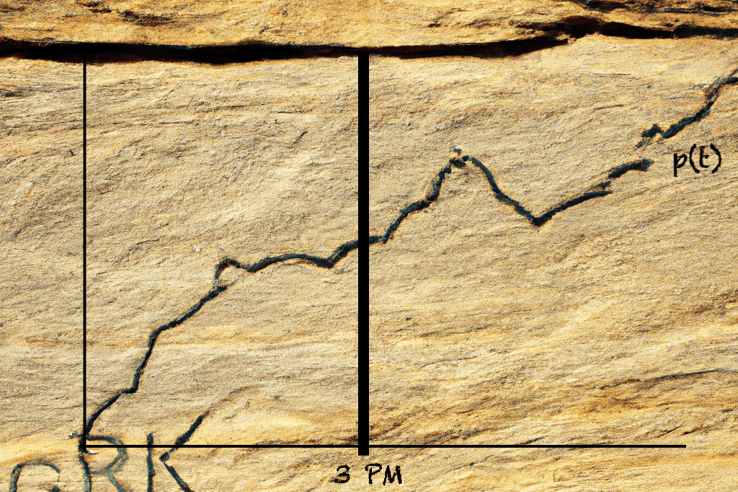
The caterpillar rolled his eyes and cleared his throat, “hrmph hrmph hrmph, At Most has this all wrong. Equal To is always on time because he is the function p(t), promptness as a function of time.” The caterpillar pointed to a graph, which seemed to have been etched on a large boulder:

Alice recognized the one variable inequality graphs Mrs. Haverson was trying to teach them, but they were not traditionally vertical graphs. Alice had to turn her head to the side so that she could grasp the concept.

“No, no, no, no, no, little girl!” grumbled the catapillar.

Alice did not particularly like being called ‘little girl’ by a caterpillar.

“You must turn your head the other way. If you turn the graph clockwise you orient it properly.”

“Yes, Mr. Caterpillar, but since I cannot turn the rock clockwise, I must turn my head counterclockwise to get that same effect.”

After much grumbling and odd twisting and bending of the caterpillar’s body segments, he agreed that she was right. “See here,” the caterpillar pointed to the graph, “someone who is overprompt is early, they are above the promptness line (p(t), that is)” the caterpillar said the last part a bit under his breath, “for they reached their destination prior to the intended time. The underprompt person is late because they have not arrived at their destination on time. So you see, At Most is either always on time, or late,” finished the caterpillar.

“Like I said, I’m either on time or late, my brother is either on time or early, the rabbit is only on time, and the Queen does whatever she likes.” At Most smiled with satisfaction.

Alice was not convinced of this explanation. “How can promptness be a function of time, unless it is also a function of position?”

“My dear, (isn’t that cute)” chortled the caterpillar, “your 3-dimensional logic won’t get you anywhere. You cannot be prompt unless you are in the right place at the right time, so the rabbit lumps promptness and position together, it’s the assumption you are in the right place at a given time. Where you need to be is arbitrary, whether you are prompt or not is always true.”

Alice was not sure she agreed, so she rolled her eyes and said, “well, I suppose I might be late to wherever it is I need to be, so I will be leaving you now.” She ran to get away from the jumble of inequality signs that continued to try to figure out how to un-jumble themselves back to their original order. She soon became tired and had to sit down and rest for a bit.

And that is the end of the excerpt. I want to unpack the graph on the boulder for a minute. The intention here is to consider single variable inequalities vertically as a way to transition to two variable inequalities that may be graphed. I find that without engaging with students conceptually, they may struggle to make meaning from y<3x+1. By having a conversation about this ridiculous example about promptness and whether someone can be over prompt or under prompt, at least can begin the conversation with students about how to make sense of these kinds of inequalities. This is to say, I'm not convinced that the caterpillar is correct or incorrect, but I can envision a lively debate about it in the classroom that could lead students to conceptually connect with the ideas at play.

Demos visual